Before I jump into algorithms, I need to understand data structures. Here’s a list of them:
- Arrays
- Linked lists
- Trees
- Stacks & Queues
- Heaps
- Hash tables
- Graphs
- Disjoint set
I know there are some more, these are just the ones I need to understand starting off.
To start, I’ll be going over the basics of each structure just to get acquainted with them.
First, we have to understand the 2 main types of data structures, linear and nonlinear. Those kinda speak for themselves, but I’ll explain more as we unpack each structure. There are 2 subtypes of linear structures, static and dynamic, which mainly pertain to their memory sizes. One is fixed and one is flexible m
Array
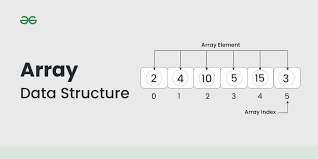
Arrays are a linear set of elements. Each element’s place is called an index. You can look at it like a flight of stairs that holds whatever item you set on each step. If you want to retrieve that item, you call it by the step it’s on, which is the index. Or you can look at it like those pill sorters with the days of the week on them. If you’re not sure which pill you take on a certain day, you simply open the lid of that day (the index), and look at what pills are in there (the elements).
This is the simplest form of information container. It’s static, so the number of elements is determined at the time of creation. You can change the values of an element, but you can’t add or remove any. There are also dynamic arrays too, which do allow for this. So they obviously sound better. Just like lists vs tuples in Python or floating points vs integers in SQL, even though one is clearly more flexible, it takes more memory (space). So it’s ok to stick with the fixed version if we know the number of elements is permanent.
Lastly, arrays come in different dimensions. 1D is a horizontal line of blocks, a single row.
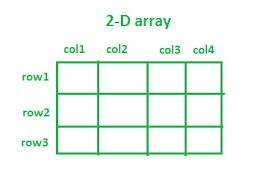
2D is a grid or matrix with rows and columns.
And 3D is a set of multiple 2Ds.

Linked List
There are 4 types of linked lists: singly, doubly, circular, and circular doubly.
Singly
A singly linked list is made of a line of 2-section boxes called nodes. The first node is called the head, and the last is the tail. The first section of the node is the data element and the second section is the pointer where it says ‘next’.
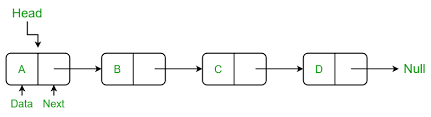
Now since it’s a linked list, it doesn’t allow for random access. In arrays, we can access any element by calling its index and ignoring the other ones, which is random access. In linked lists, if we want to call an element, we have to start from the head node and work our way down to the one we’re looking for. This is called traversing. And singlys are unidirectional, meaning they can only traverse from the head to the tail, from left to right.
Doubly
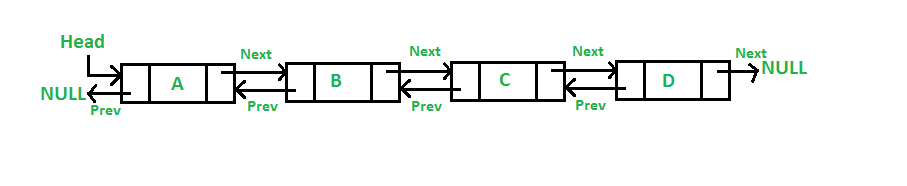
A doubly has an extra section for a previous pointer. This allows bidirectional traversing, it can start from a middle node and move forward or backward. So this is a form of random access, but not as explicit as an array’s. We’ll get into the technicalities later.
Circular
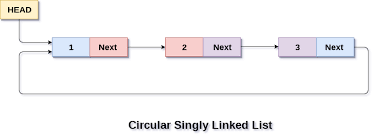
A circular linked list is an extension of a singly. Once it reaches the tail node, it circles back to the head. This is used for a singly that requires a loop, especially for real-time applications. Since it loops, there is no null. A main concern with circulars is they need to be manually stopped, or else they’ll loop indefinitely.
Doubly Circular

Doubly circulars are self-explanatory since I’ve gone through the others. In terms of their application, I’m not yet sure what they’d be used for.
Stacks & Queues
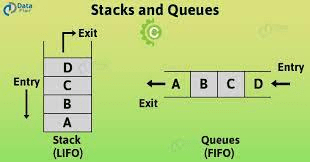
A stack is a linear structure that vertically contains data. Like a stack of books, it follows a last-in-first-out principle (LIFO). Whichever is on top, is the one to get replaced. Adding an element to the stack is called a push and removing it is a pop.
A queue is similar, except it’s horizontal and it follows a first-in-first-out (FIFO) principle. Visually, it looks the same as an array, but they’re used in different ways. Stacks and queues don’t have indices like arrays, you can’t directly access an element in the middle. A queue’s first (leftmost) element is considered the front, and the last (rightmost) is the rear. With a row of books, if you enqueue (add) a book to the rear, you must dequeue (remove) a book from the front.
Disjoint Set

Disjoint means 2 or more sets have no elements in common. No overlap.
All I can say about it now is it’s used to manipulate sets of elements without mixing them up. It uses a variety of union techniques to pick out the overlaps and evaluate what to do with them. It’s a lot more than that but we’ll have to expound on it in a separate post.
Hash Tables
Hash tables are an advanced form of arrays. I’ve been trying hard to simplify the differences. All I can say for now is they allow random access, which means faster lookup, and they take up more memory. The other difference will require me to explain some of the properties I listed. So we’ll to get to this later.
Trees
Trees are a nonlinear structure that follow a parent-child hierarchy.
The most basic tree is a binary tree. It’s binary because each node only has 2 children at most.
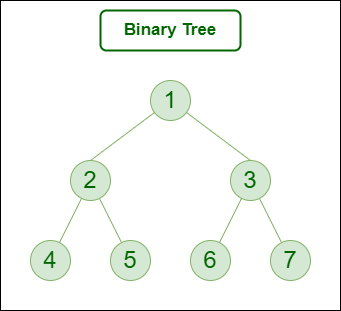
The first node is called the root, which is the parent. 2 and 3 are its children, thus they’re siblings. These may also be called the ‘left’ and ‘right’ child.
There’s a ternary tree where each node has 3 children.
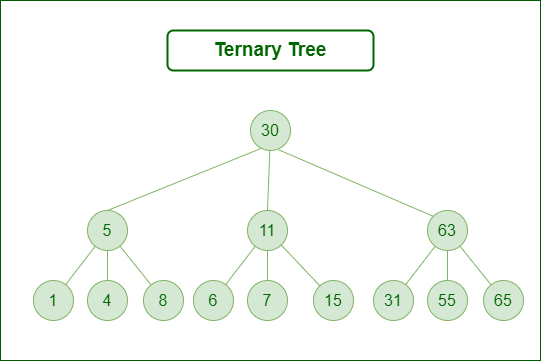
And there’s an n-ary tree which means each node can have a varied number of children.

Any node that doesn’t have a child is called a leaf.
There are variations of trees too but we’ll get to those in a separate post
Heaps
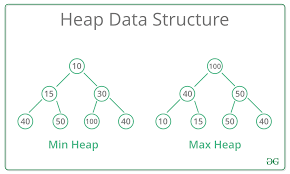
A heap is more of an advanced method of dealing with trees. It’s not a separate data structure. It deals with a heap property which is prioritizing certain elements. Mainly the parent nodes that are less or greater than their children. Its main purpose is efficient extraction. We’ll elaborate on its other functions later.
Graphs
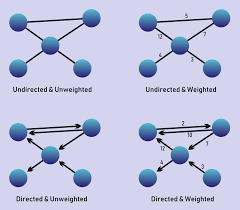
There are a handful of types of graphs so we’ll start with the main types: directed and undirected, weighted and unweighted.
All graphs are made of nodes and edges (or vertices and links). The nodes are the actual data elements and the edges are the relationship between elements. Directed edges have a one-way relationship. A may follow B, but it doesn’t mean B follows A. Undirected means the relationship is mutual, where A follows B and B follows A. Weighted edges add a value to the relationship, like the number of times 2 accounts have interacted or how much money they’ve sent to each other. Unweighted implies that all nodes are equal.

Now that I got the basic structures down, I’m going to jump into algorithm analysis.